You can generate a set of random numbers in SAS that are uniformly distributed by using the RAND function in the DATA step or by using the RANDGEN subroutine in SAS/IML software. (These same functions also generate random numbers from other common distributions such as binomial and normal.)
The syntax is simple. The following DATA step creates a data set that contains 10 random uniform numbers in the range (0,1):
data A; call streaminit(123); /* set random number seed */ do i = 1 to 10; u = rand("Uniform"); /* u ~ U(0,1) */ output; end; run; |
The syntax for the SAS/IML program is similar, except that you can avoid the loop (vectorize) by allocating a vector and then filling all elements by using a single call to RANDGEN:
proc iml; call randseed(123); /* set random number seed */ u = j(10,1); /* allocate */ call randgen(u, "Uniform"); /* u ~ U(0,1) */ |
Random uniform numbers in the interval (a,b)
If you want generate random decimal numbers in the interval (a,b), you have to scale and translate the values that are produced by RAND and RANDGEN. The width of the interval (a,b) is b-a, so the following statements produce random values in the interval (a,b):
a = -1; b = 1; /* example values */ x = a + (b-a)*u; |
The same expression is valid in the DATA step and the SAS/IML language.
Random integers in SAS
You can use the FLOOR or CEIL functions to transform (continuous) random values into (discrete) random integers. In statistical programming, it is common to generate random integers in the range 1 to Max for some value of Max, because you can use those values as observation numbers (indices) to sample from data. The following statements generate random integers in the range 1 to 10:
Max = 10; k = ceil( Max*u ); /* uniform integer in 1..Max */ |
If you want random integers between 0 and Max or between Min and Max, the FLOOR function is more convenient:
Min = 5; n = floor( (1+Max)*u ); /* uniform integer in 0..Max */ m = min + floor( (1+Max-Min)*u ); /* uniform integer in Min..Max */ |
For convenience, you can define a macro that returns a random integers between two values. Again, the same expressions are valid in the DATA step and the SAS/IML language.
Putting it all together
The following DATA step demonstrates all the ideas in this blog post and generates 1,000 random numbers in SAS. The values are uniformly distributed with various properties:
%let NObs = 1000; data Unif(keep=u x k n m); call streaminit(123); a = -1; b = 1; Min = 5; Max = 10; do i = 1 to &NObs; u = rand("Uniform"); /* decimal values in (0,1) */ x = a + (b-a)*u; /* decimal values (a,b) */ k = ceil( Max*u ); /* integer values in 1..Max */ n = floor( (1+Max)*u ); /* integer values in 0..Max */ m = min + floor((1+Max-Min)*u); /* integer values in Min..Max */ output; end; run; |
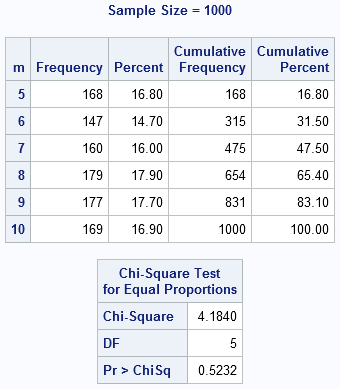
You can use the UNIVARIATE and FREQ procedures in Base SAS to see how closely the statistics of the sample match the characteristics of the populations. The PROC UNIVARIATE output is not shown, but the histograms show that the sample data for the u and x variables are, indeed, uniformly distributed on (0,1) and (-1,1), respectively. The PROC FREQ output shows that the k, n, and m variables contain integers that are uniformly distributed within their respective ranges. Only the output for the m variable is shown.
proc univariate data=Unif; var u x; histogram u/ endpoints=0 to 1 by 0.05; histogram x/ endpoints=-1 to 1 by 0.1; run; proc freq data=Unif; tables k n m / chisq; run; |
In summary, use the RAND("uniform") call to generate random numbers in SAS. By scaling and translating these values, you can obtain random values (decimal or integer) on any interval.
If you just want random integers between two values, see the article "How to generate random integers in SAS."
WANT MORE GREAT INSIGHTS MONTHLY? | SUBSCRIBE TO THE SAS TECH REPORT

56 Comments
I wonder what kind of algorithm does SAS use when generating random numbers?
SAS uses the Mersenne-Twister random number generator: http://support.sas.com/documentation/cdl/en/lefunctionsref/63354/HTML/default/viewer.htm#p0fpeei0opypg8n1b06qe4r040lv.htm
I use RANUNI. Is there a differnece?
Yes, they are different. RANUNI, RANNOR, etc., are functions that use an older random number generator. Their statistical properties are not as good as the newer RAND function. ("Newer" means it's only been in SAS since the mid-1990s!) For small data sets and simple demo examples, it doesn’t matter which function you use. However, if you are doing serious Monte Carlo simulations and generating millions of random numbers, then the better statistical properties of the RAND function become important.
Hi Rick,
I am using VNORMAL for Monte Carlo simulations at the moment. Do you know which random number generator this function is using? I can't find anything in the SAS manual. Would it be better to use RANDNORMAL? I know RANDNORMAL allows you to use RANDSEED and VNORMAL doesn't but I didn't deem this very important.
VNORMAL uses the older random number generator, which has a period of about 2 billion. It's fine if you are generating fewer than a billion random numbers. For huge Monte Carlo simulations, it's safer to use RANDNORMAL. I blogged about the RANDNORMAL module at http://blogs.sas.com/content/iml/2011/01/12/sampling-from-the-multivariate-normal-distribution/
Pingback: Random number streams in SAS: How do they work? - The DO Loop
Pingback: Readers’ choice 2011: The DO Loop’s 10 most popular posts - The DO Loop
Hi Rick,
Thank you for the interesting and very helpful writings on SAS random numbers.
I ran 36 instances of a SAS program in parallel on a cluster. I provided unique seed to each running instance. Every instance generated 4,000,000 (four million) random numbers using RANUNI. Total of 144,000,000 (=36 * 4 mln.) random numbers for all instances were needed. After all instances have completed, I noticed that about 2.8% of the random numbers (generated in all instances) were duplicated, even though unique seeds were used by the instances.
When I used STREAMINIT and then RAND("UNIFORM") to generate the random numbers, about 4% of the random numbers (generated in all instances) were duplicated.
Your comments are greatly appreciated.
If you haven't yet read my post Random Number Streams in SAS: How do they work?, be sure to read it.
In general, you shouldn't confuse INDEPENDENCE with UNIQUENESS. Random number generators try to achieve independence. There is nothing intrinsically wrong with getting a repeated value, just like there is nothing wrong with rolling a die and getting the same value multiple times. It happens often, and it doesn't mean that the die is unfair.
I caution against using RANUNI for large samples. RANUNI only provides 2 billion possible values. If you generate 144m obs in RANUNI, you shouldn't be surprised to get a repeated value. This is the famous Birthday Matching Problem, which I blogged about in the form of matching initials at a meeting.
I am curious: how are you determining that values are duplicated. PROC FREQ? PROC SORT with the NODUP option?
Hi Rick,
Thank you for the reply. I read your post - it is interesting and helpful. Thanks.
Please note, that when I use only one seed and generate 144m random numbers, I do not see any duplications.
Here is how I determine if that values are duplicated or not:
1. Assuming that every generated random number is placed (printed out) on a separate line of a file, for instance rand_nums.lst.
2. cat (Linux) command counts the number of all lines in the file. For instance:
cat rand_nums.lst | wc -l
3. sort (Linux) command counts the number of unique lines, For instance:
sort -nu rand_nums.lst | wc -l
4. If these number are the same then this means that the generated random numbers are unique.
When you say there are no duplicates when you use one seed, is this for RANUNI, RAND, or both?
So far I have tried only RANUNI.
Pingback: How many observations were processed by that last step? - The SAS Dummy
Pingback: Generating a random orthogonal matrix - The DO Loop
How could I randomly generate a uniformly distributed variable, for example RAN, which always falls between 0 and 2?
See the section, "Random uniform on the interval [a,b]" at the top of the page. For you, a=0 and b=2 so
ran = 2*u;
Hi Rick Wicklin,
I am a Danish master student. I am currently struggling with a simulation for my master thesis. The purpose of the simulation is to verify wether industrial merger waves exist in Europe or not.
I need to randomly generate x uniformly distributed numbers ('pseudo'-M&A's) between 1 and 120 (JanYear1, FebYear1...DecYear10) for every identified M&A-active industry (48 industries). And I need to repeat this step 1000 times. x is the observed number of M&A's in the industry under investigation.
- based on this blog post, I now think I know how to conduct the simulation in SAS.
My hurdle is that after the simulation process, I need to identify the volume of the highest 24-month concentration for each of the 1000 draws. Can you help me here, Rick? I need the 24-month concentrations to conclude whether an industrial merger wave exists or not for a given industry --> if in 99% of the draws the highest 24-month concentration is lower than the actually or observed peak concentration, there is significant evidence for the existence of an 2 year merger wave within the given industry, in that decade.
I really, really hope that you can help me.
Hi Rick,
the above code is not generating unique random numbers if set number of observations=400000 and min=10000000 and max=99999999. Basically I need to generate unique random number with 8 digit.
any alternatives?
Random numbers are not necessarily unique. Consider rolling a six-sided die two times. About 1/6 of the time the random number 1-6 will be repeated! To get uniqueness you want to "sample without replacement" from the list of numbers that you want. You can use the METHOD=SRS method in PROC SURVEYSELECT to select samples without replacement. In PROC IML, you can use the SAMPLE function.
Hi Rick! Is it possible to use the RAND() function inside PROC IML? I tried doing that and it seems to work; I'm just concerned if it produces the same result as the RANDGEN subroutine. I've been reading some comments that inside PROC IML, the RANDGEN subroutine should be used. However, I don't need to generate one stream of random numbers every iteration. I need to generate just one random number, and the parameter of the distribution (say the binomial sample size) varies from iteration to iteration, so you can see my dilemma about using RANDGEN.
I do not see your dilemma about using RANDGEN. You can geneate 1 sample as efficiently with RANDGEN as with RAND. However, to answer your question: yes, you can call RAND from PROC IML. Furthermore, you can pass a vector of parameters to RAND and get out a vector of binomial sample sizes.
Pingback: Popular! Articles that strike a chord with SAS users - The DO Loop
Hi..,
How to generate 5 sample with sample size is seven by using SAS?
From what distribution? Uniform? Discrete uniform? Normal? I've written more than 30 articles on simultion, so you can find lots of examples by clicking on the "Simulation and Sampling" link in the right-hand sidebar. In particular, look at the DATA step in the second set of code in this article: http://blogs.sas.com/content/iml/2012/07/18/simulation-in-sas-the-slow-way-or-the-by-way/ It shows a DATA step with two nested loops. Make the outer loop go to 5 and the inner loop go to 7.
Hello,
I was wondering if it's possible to do a similar exercise, but pulling a VECTOR of 2 bivariate normal variables? If I know the means and the variance-covariance matrix of my variables, can SAS randomly draw from the joint distribution?
Thanks!
Josh
Yes, you can sample from the multivariate normal distribution by using the RANDNORMAL function in SAS/IML software. SAS also supports other multivariate distributions.
Can random number generation/simulation be used in Proc OPTMODEL ? i know it is supported in proc model to do the simulation, but could not find anything for Proc Optmodel.
There's one example here: http://support.sas.com/documentation/cdl/en/ormpug/63352/HTML/default/viewer.htm#ormpug_optmodel_sect020.htm
How can randomly select when your data is from 2003- 2013 and we will select only for 2003-2012.what syntax do we need to use?
Sounds like you want to subset the data by using a WHERE clause
WHERE YEAR>=2003 AND YEAR<=2012;
Then
m = 2003 + floor((1+2012-2003)*u); /* uniform integer in 2003..2012 */
Hi Rick,
Sorry to revive an old thread, but I was wondering what your thoughts were (and why it wasn't mentioned) on using ROUND() around the a+(b-a)*u formula for random integers in [a,b]? I originally used FLOOR()/CEIL() in my code, but lately (especially when I have a small interval, such as [1,5]) I have switched to ROUND() since FLOOR()/CEIL() bias away from b/a, respectively. I know that traditional discrete uniform distribution says that random draws of each value in an interval of K values should tend towards a 1/K distribution, but I don't believe the FLOOR()/CEIL() functions provide this.
Thanks for all of the great knowledge that you share,
Ben
Maybe I am misunderstanding what you are proposing. I didn't put ROUND around the a+(b-a)*u formula because the resulting integers are not uniformly distributed. For example, if I want uniform integers in the range {1,2,3,4,5}, it is incorrect to write the following:
a = 1; b = 5;
u = j(10000,1); /* allocate */
call randgen(u, "Uniform"); /* u ~ U[0,1] */
p = round(a + (b-a)*u); /* NOT uniformly distributed! */
call tabulate(value, freq, p); /* compute empirical distribution */
print (freq/10000)[c=(char(value)) f=percent7.4];
The code shows that the chance of a 1 or 5 is only 12.5% each, whereas the chance of 2, 3, or 4 is 25% each.
Rick: is there a way to generate random numbers with a specified (with known (geo)mean and (geo)sd) lognormal distribution in SAS? Many thanks for the blog.
If I understand you, use the RAND("Normal", mu, sigma) function to generate X ~ N(mu, sigma). The variable Y = exp(X) is lognormally distributed with parameters mu and sigma.
Implementing the formulas for mu and sigma from the "Notation" section of the "Log-normal distribution" entry on the Wikipedia (http://en.wikipedia.org/wiki/Log-normal_distribution)
and with your suggestion the following syntax:
produced the data set with the MEAN = 81.2260929 and SD = 15.6965921
what is very close to the magnitudes wanted :) !
Please correct me if I have a mistake.
Thank you again for the blog --- very informative and practically useful.
P.S.
Initially I meant what I was suggested
(http://stackoverflow.com/a/23635776/1009306)
and unexpectedly what was written about by yourself
(http://blogs.sas.com/content/iml/2013/07/22/the-inverse-cdf-method/)
Does the iCDF approach give the same results? What are the benefits to use it?
Looks good, although I'd use lgnrm = exp(nr) in the DATA step and set THETA=0 in the HISTOGRAM stmt.
If you have more questions, please post to the SAS Support Communities. There are about 20 subcommunities there, such as SAS Statistical Procedures.
The advantage of the iCDF method is that is always works. However, it tends to be slower than direct transformation methods, such as used here.
Thank you for your suggestions and quick replies :).
Thanks. I used this today for a demonstration I was working on of uniform and normal distributions.
Code to generate random numbers between 0 and 1 continuous distribution c programming language
Hi
I have a dataset for a one district in this district 16 Mandal and each Mandal have three type (Govt., Private, NGO,) 3500 school, I want a sample for each Mandal 1 got 1 private 1 NGO School total Number of sample are 48, whenever we run the programme the sample should be different, not same , could you help me how can I take a sample using SAS
It sounds like you should look at PROC SURVEYSELECT. Post your question and example data to the SAS Support Communities.
Pingback: How to generate random integers in SAS - The DO Loop
RANDOMIZED SERIAL/SEQUENTIAL NUMBERS (UNIQUE & UNPREDICTABLE)
If only the random numbers are allowed to be of unique value.
12345678900 72
12345678901 34 . 12345678926 34. 12345678951 24 . 12345678976 84.
12345678902 65. 12345678927 63. 12345678952 51. 12345678977 67.
12345678903 09. 12345678928 11. 12345678953 19 . 12345678978 53.
12345678904 22 . 12345678929 44. 12345678954 78. 12345678979 04.
12345678905 21. 12345678930 85. 12345678955 76. 12345678980 35.
12345678906 37. 12345678931 01. 12345678956 31. 12345678981 73.
12345678907 42. 12345678932 55. 12345678957 12. 12345678982 16.
12345678908 20 . 12345678933 95. 12345678958 87. 12345678983 77.
12345678909 71. 12345678934 49. 12345678959 83. 12345678984 13.
12345678910 32. 12345678935 60. 12345678960 50 . 12345678985 45.
12345678911 58. 12345678936 86. 12345678961 02 . 12345678986 61.
12345678912 66. 12345678937 30. 12345678962 64. 12345678987 23.
12345678913 10 . 12345678938 48. 12345678963 94. 12345678988 40.
12345678914 79. 12345678939 89. 12345678964 27. 12345678989 70.
12345678915 93 . 12345678940 43. 12345678965 92 . 12345678990 08.
12345678916 46. 12345678941 72. 12345678966 03. 12345678991 88.
12345678917 57. 12345678942 14. 12345678967 47 . 12345678992 65.
12345678918 52. 12345678943 38 12345678968 62. 12345678993 17.
12345678919 15. 12345678944 75. 12345678969 80. 12345678994 54.
12345678920 41. 12345678945 07. 12345678970 18. 12345678995 28.
12345678921 62. 12345678946 25. 12345678971 58. 12345678996 74.
12345678922 26 . 12345678947 69. 12345678972 43. 12345678997 29.
12345678923 91. 12345678948 82. 12345678973 59 . 12345678998 33.
12345678924 05 . 12345678949 56. 12345678974 81. 12345678999 78.
12345678925 36. 12345678950 68. 12345678975 90 . 12345679000 06.
These are 101 unique random numbers. Each number consists of 13 digits, out of which first 11 digits are sequential numbers and the 12th and 13th digits together form a random number.
These last two digits transform the 11 digit sequential number into a 13 digit random number. Thus when a sequential number is transformed into a random number by addition of 1 or 2 digits, such randomization does not need math based algorithm.
Even if the two digits are created by math based algorithms, there can be innumerable such algorithms that can create two digit random numbers.
Hence, my claim is that when 1, 2 or 3 randomly created digits are attached to the sequential number, you award randomness to it and such randomized sequential numbers are unpredictable.
Thus a SHORTEST POSSIBLE sequence of 11 digits can accommodate one billion unpredictable random numbers and a sequence of only 14 digits can accommodate one trillion unpredictable random numbers.
Hello,
Please correct your notation of the range regarding the RAND function uniform distribution. According to SAS 9.3, the range is 0 < x < 1, indicating it should be noted as (0, 1)
Thank you.
Is there a way to generate low-discrepancy Sobol sequences?
I suggest you post your questions to the SAS Support Communities and indicate what you are trying to accomplish.
please there is a range of numbers from 0-99.The number 98.40 is the integer i want to get.How do i know when exactly the 98.40 will occure and how many times can i get this number .
The number 98.40 is not an integer. If you are generating random integers in [0,99], then a particular integer (say, 98) will occur ON AVERAGE about 1% of the time, but you cannot predict when it will occur or how often it will appear in a particular sample. If you have more questions, please ask at the SAS Support Communities.
Hello,
I remember i asked a question about generating random number with normal distribution and also require them within two numbers. E.g., numbers with 2 to 200 with a normal distribution of mean 90 std 10. Could you send me the link to this question again?
Best,
Mei
Look for the article about the "eyeball distribution."
Thank you very much!
Hi Rick:
The article you wrote is very helpful.
One thing puzzles me is that I'm trying to generate random number using SAS rand function using the same seed, yet, I'm getting different output from which I'm comparing. Any thoughts\comments\suggestions?
Thank you in advance.
I would have to know more information, such as what numbers are you comparing, how were they generated, are they from the same version of SAS, etc. I suggest you post your question to the SAS Support Communities. Include your program and the details above. You can tag me (@Rick_SAS) to make sure I am notified when it posts.
Hi Rick,
For someone who is new to programming, what is the best way to learn SAS? I will utilize it in my future work and although I am taking a class on it, the information is coming at me faster than I can grasp it so I want to know some tips on how to learn it on my own. Thank you.
My advice: the best way to learn ANYTHING is to practice it regularly. So if you want to become a better programmer, you need to write a lot of programs. I'll add that you should always break a complex problem into a sequence of simpler steps. Good luck!