There's "big," and then there is "factorial big."

If you have k items, the number of permutations is "k factorial," which is written as k!. The factorial function gets big fast. For example, the value of k! for several values of k is shown in the following table. You can use a custom algorithm to compute accurate, extended-precision values of the factorial function for k>18.

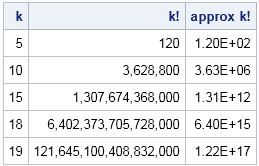
Base SAS has several functions for working with permutations, including the ALLPERM function (which generates all permutations of k items) and the RANPERM function (which generates a random permutation of k items). The documentation for the ALLPERM function mentions that you can specify no more than 18 items. That is, it only enables you to compute all permutations when k≤ 18.

A SAS programmer recently asked why k=18 is the limit in these factorial computations. At first glance, 18 does seem to be an unusual choice. Why not k=16, since computer scientists love powers of 2? Or why not k=20, since most of us count in base 10?

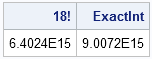
The explanation is that k=18 is the largest value for which k! can be represented by an 8-byte integer. The first argument to the ALLPERM function is an index that enumerates the permutation, and this argument does not fit into an 8-byte integer when k>18. You can use the CONSTANT function in SAS to find the value of the largest 8-byte integer:

data _null_;
Fact18 = fact(18);
ExactInt=constant("exactint");
put Fact18=;
put ExactInt=;
run;

From a programming perspective, having a limit also prevents us programmers from accidentally creating a loop that iterates a billion billion times (which is 20!). When dealing with permutations and combinations, implementing a smart algorithm is almost always preferable to a brute-force computation that iterates over every possible permutation.

Do you have any tales of woe from when you inadvertently tried to compute with a large combinatorial number? Leave a comment.