Gambling games that use dice, such as the game of "craps," are often used to demonstrate the laws of probability. For two dice, the possible rolls and probability of each roll are usually represented by a matrix. Consequently, the SAS/IML language makes it easy to compute the probabilities of various events.
For two fair dice, the probability of any side appearing is 1/6. Because the rolls are independent, the joint probability is computed as the product of the marginal probabilities. You can also create a matrix that summarizes the various ways that each particular number can occur:
proc iml;
dieProb = j(1, 6, 1/6); /* each die is fair: Prob(any face)=1/6 */
/* joint prob is indep = product of marginals */
probs = dieProb` * dieProb; /* 6x6 matrix; all elements = 1/36 */
events = repeat(1:6, 6) + T(1:6);
print events[c=("1":"6") r=("1":"6")]; |
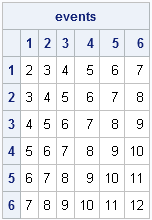
You can use the event and probs matrices to compute the probabilities of each possible sum of two dice. There are several ways to do this, but I like to use the LOC function to find the elements of the event matrix that correspond to each roll, and then add the associated probabilities:
P = j(1, 12, 0); /* probability of each event */
do i = 2 to ncol(P);
idx = loc( events=i );
P[i] = sum( probs[idx] );
end;
print P[format=6.4 c=("P1":"P12")]; |

The preceding table shows the probabilities of each roll. (Note that the probability of rolling a 1 with 2 dice is zero; the P[1] element is not used for any computations.) You can use the table to compute the probability of winning at craps. If you roll a 7 or 11 on the first roll, you win. If you roll a 2, 3, or 12, you lose. If you roll a 4, 5, 6, 8, 9, or 10 on the first roll (called "the point"), you continue rolling. You win if you can successfully re-roll your "point" before you roll a 7. It is an exercise in conditional probability that you can compute the probability of making a "point" in craps by summing a ratio of probabilities, as follows:
win = {7 11};
lose = {2 3 12};
point = (4:6) || (8:10);
Pwin1 = sum( P[win] ); /* Prob of winning on first roll */
PLose1 = sum( P[lose] ); /* Prob of losing on first roll */
/* Prob winning = Pr(7 or 11) + Prob(Making Point) */
Pwin = P[7] + P[11] + sum(P[point]##2 / (P[point] + P[7]));
print Pwin1 PLose1 Pwin; |
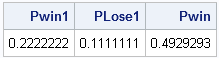
According to the computation, the probability of winning at craps is almost—but not quite!—50%.
This exercise shows that having a matrix and vector language is useful for computing with probabilities. More importantly, however, this post sets the foundations for looking at the interesting case where the two dice are not fair. If you change the definition of dieProb (on the first line of the program) so that it is no longer a constant vector, all of the computations are still valid!
Next week I will post an article that shows how the odds change if some sides of the dice are more likely to appear than others. Feel free to conduct your own investigation of unfair dice before then.

7 Comments
>>>If you roll a 7 or 11 on the first roll, you win. If you roll a 2, 3, or 11, you lose.
Ths should be "...If you roll a 2, 3, or 12, you lose."
Thanks. Corrected.
While the odds shown above are fairly generic, the game really rests on chip management, balancing a Pass/Don't Pass game, and sizing up the rollers.
Craps players know that the come out (first) roll favors them, but many play a "Don't Pass" strategy when a point has to be made, especially with longer odds (a point of 4 or 10).
Even Don't Pass players will hedge with early bets on 6 or 8, then then turn off these bets after the first point rolls. Hedging shrinks an overall gain, but who wouldn't want to play a positive margin?
Study up, or give it up.
Of course there is much more to playing craps, than just knowing the base probabilities, primarily because the house payouts are less than the event probabilities. This post does not discuss betting strategies or the expected return of various bets. For people who actually play craps, there are many Web sites that discuss these issues.
"If you roll a 2, 3, or 11, you lose."
Should be 2, 3, or 12. More importantly, the code is correct :)
Pingback: Playing “craps” with unfair dice - The DO Loop
Pingback: Dice and the correctness of a simulation - The DO Loop