Like most programming languages, the SAS/IML language has many functions. However, the SAS/IML language also has quite a few operators. Operators can act on a matrix or on rows or columns of a matrix. They are less intuitive, but can be quite powerful because they enable you perform computations without writing a DO loop. This article describes the elementwise minimum and maximum operators.
Recently I wrote about how to use subscript operators to compute the min or max of a row or column of a data matrix. These min/max operators are two examples of subscript operators that perform row and column operations on a data matrix. Other subscript operators enable you to compute the sum, mean, and sum of squares for rows or columns of a matrix.
But what if you need to compare the values across two different matrices? To paraphrase a popular ad campaign, "there's an op for that!"
The elementwise minimum operator
Here's an example that illustrate how the elementwise minimum operator works. Suppose that there is a teacher who always gives a bonus question on her quizzes and tests. Quizzes are worth 50 points, tests are worth 100 points, and the bonus question is worth 5 points. However, the teacher does not allow any student to score more than 50 points on a quiz or more than 100 points on a test.
The following SAS/IML statements define the raw scores for three students in the class:
proc iml;
Test = {"Quiz1" "Test1" "Quiz2" "Test2"};
Name = {"Rita", "Sam", "Tim"};
x = {55 105 50 105,
45 95 55 90,
15 100 55 105};
print x[r=Name c=Test L="Raw Scores"]; |
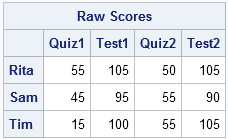
You can see that on several occasions a student has answered all questions correctly, including the bonus question. The teacher wants to cap the scores at some maximum value. The elementwise minimum operator (><) is an easy way to perform this operation. To ensure that 100 is the maximum possible score, the teacher could apply the >< operator, just as in the SAS DATA step:
trunc100 = x >< 100; /* result is minimum of x[i,j] and 100 */ print trunc100[r=Name c=Test L="Max Score = 100"]; |
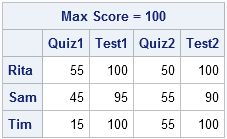
Now the maximum value of any cell is 100. However, columns 1 and 3 represent quiz scores, so they need to be truncated at the maximum value of 50. You might be tempted to loop over the columns and use the CHOOSE function to cap the maximum value of each column, as follows:
target = {50 100 50 100}; /* target[i] is max allowed value of column i */
A = j(nrow(x), ncol(x)); /* allocate new matrix for results */
do j = 1 to 4;
A[,j] = choose(x[,j] > target[j], target[j], x[,j]);
end; |
However, the elementwise minimum operator enables you to compute the result without writing a loop. Because the target vector is a row vector with four columns, the following statement returns a matrix where element (i,j) is the minimum of A[i,j] and target[j]:
A = (x >< target); /* target[j] is max allowed value of column j */ print A[r=Name c=Test L="Adjusted Scores"]; |
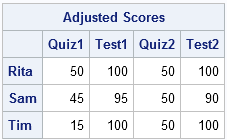
The elementwise maximum operator
In a similar way, the elementwise maximum operator (<>) enables the teacher to set the smallest possible value for a test score. The teacher might decide that extremely low scores are unduly influential when computing the average grade, so she might decide to make 25 the lowest possible score, as follows:
B = A <> 25; /* result is maximum of A[i,j] and 25 */ |
The elementwise minimum and maximum operators work when the second matrix is a scalar, a row vector, a column vector, or a matrix.
- The expression (A >< scalar) returns a matrix that is the same size of A, and no element is smaller than scalar.
- The expression (A >< row_vector) returns a matrix that is the same size of A, and no element of the jth column is smaller than the jth element of row_vector.
- The expression (A >< col_vector) returns a matrix that is the same size of A, and no element of the ith row is smaller than the ith element of col_vector.
- The expression (A >< matrix) returns a matrix that is the same size of A, and the (i,j)th element is no smaller than the (i,j)th element of matrix.
Truncating vector values
The elementwise min/max operators can be used to truncate a vector of values. This often comes up when data has small negative values (possibly because of numerical round off) and you want to truncate all negative values to 0.
Another example is when you want to truncate the values of a function. For example, the sine function returns values in the range [–1, 1]. If you want to truncate the sine function at ±1/2, you can use the following shorthand notation:
ods graphics / width=400px height=200px; t = do(0,12.56,0.03); z = (-0.5 <> sin(t) >< 0.5); /* truncate within [-0.5, 0.5] */ title "Truncated Sine Function"; call series(t, z); |
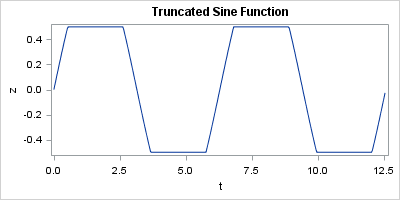

1 Comment
Pingback: Avoid loops, avoid the APPLY function, vectorize! - The DO Loop