The other day I was constructing covariance matrices for simulating data for a mixed model with repeated measurements. I was using the SAS/IML BLOCK function to build up the "R-side" covariance matrix from smaller blocks. The matrix I was constructing was block-diagonal and looked like this:
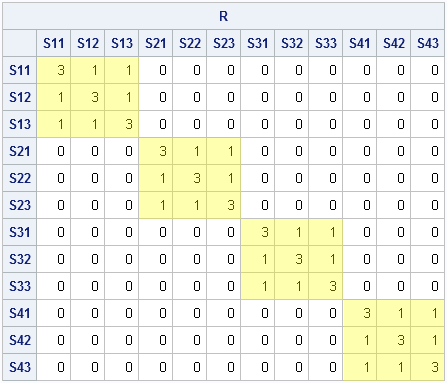
The matrix represents a covariance matrix for four individuals where each individual has three repeated measurements and where the measurements for each individual exhibit a compound symmetric covariance structure.
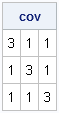
To construct the block-diagonal matrix, the first step is to construct the little 3x3 compound symmetric matrix, as follows:
proc iml; k=3; /* number of measurements per individual */ b = j(k,k,1) + 2*I(k); /* residual cov=1; common cov=2 */ print b[label="cov"]; |
To simulate data for multiple subjects, it is common to build R, a big block-diagonal matrix such that each block equals b. This matrix is shown at the top of this post. I initially used the BLOCK function to constructs the covariance matrix, as follows:
s=4; /* number of individuals */ R = b; /* block diagonal: one kxk block for each indiv */ do i = 2 to s; R = block(R,b); end; print R; |
That works, and the BLOCK function is good to know about, but I recently realized that there is a more efficient way to construct a block-diagonal matrix. Calling the BLOCK function in a DO loop is unnecessary! The SAS/IML language supports the direct product (Kronecker product) operator, @. This is not an operator that I use every day (or even every year!), but it turns out that this operator makes it super-easy to construct block-diagonal matrices. The following statement computes exactly the same block-diagonal matrix:
/* block-diagonal matrix with s blocks, each block equals b */ R = I(s) @ b; |
I always think it is cool to discover new ways to use the SAS/IML language to avoid writing a DO loop. In any matrix-vector language (SAS/IML, R, MATLAB,...) that is a key to efficient performance. This trick to construct a block-diagonal matrix efficiently is the latest entry on my ever-growing list!

2 Comments
I recently had a similar situation where I used the Kronecker product to generate some data. Specifically, I needed to generate a series of bivariate normal datasets. Rather than specifying them individually, I used the Kroenecker product to create a large variance-covariance matrix with the block diagonals corresponding to my bivariate matrix. However, some of this efficiency has been lost because I have to use the BY statement in Proc Mixed when I analyze the datasets. Could you recommend a way to specify the repeated statement that would allow me to process the matrix in a single step(i.e. without the BY statement)? My original code looked like this:
proc mixed data=SIMDATA method=reml ;
class SubjectID Visit Trt Sim_ID;
by Sim_ID;
model Mu = Visit Trt Visit*Trt / s ;
repeated / type=ar(1) sub=zSub_StudyID ;
lsmeans Visit*Tx/diff=control('2' '1') ;
run;
I've tried changing type=Un@ar(1) but this doesn't quite give me what I'm looking for.
That's an interesting application, but if you have a single covariance matrix, there is no need to use a block structure. Use the RANDNORMAL function as shown in this example of how to generate samples from the multivariate normal distribution.
Maybe I don't understand your model, but in general there is nothing inefficient about using the BY statement (although no need to list Sim_ID on the CLASS stmt). It sounds like you are following the advice I frequently give on how to simulate data efficiently in SAS.
For details and many examples of using simulation for regression modeling, see Chapters 11-12 of Simulating Data with SAS.