I recently encountered a SUGI30 paper by Chuck Kincaid entitled "Guidelines for Selecting the Covariance Structure in Mixed Model Analysis." I think Kincaid does a good job of describing some common covariance structures that are used in mixed models.
One of the many uses for SAS/IML is as a language for statistical simulation. In simulating data for mixed models, it is necessary to know how to generate covariance structures that arise in practice. The following SAS/IML program uses Kincaid's notation and definitions (see p. 2–3) to construct some common covariance matrix structures that arise in mixed models. These functions and text are taken from my forthcoming book on Simulating Data with SAS (2013).
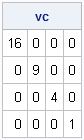
A covariance matrix with a diagonal structure
The diagonal covariance matrix is known as the variance components model. The covariance matrix that contains specified variances along the diagonal. It is easy to create such a covariance structure in SAS/IML software, as demonstrated by the following module definition:
proc iml;
/* variance components: diag({var1, var2,..,varN}) */
vc = diag({16,9,4,1});
print vc; |
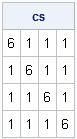
A covariance matrix with compound symmetry
The compound symmetry model is the sum of a constant matrix and a diagonal matrix. This structure forms a covariance matrix provided that the diagonal elements are large relative to the off-diagonal elements. The following module generates a matrix with compound symmetry:
start CompSym(N, v, v1); return( j(N,N,v1) + diag( j(N,1,v) ) ); finish; cs = CompSym(4, 5, 1); print cs; |
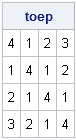
A covariance matrix with Toeplitz structure
A Toeplitz matrix has a banded structure. The diagonals that are parallel to the main diagonal are constant. If the diagonal elements are large relative to the off-diagonal elements, then the Toeplitz matrix is positive definite. The SAS/IML language has a built-in TOEPLITZ function that returns a Toeplitz matrix, as shown in the following example:
toep = toeplitz( {4 1 2 3} );
print toep; |
It is a mathematical fact that the constant correlation matrix that has all off-diagonal entries equal to ρ is positive semidefinite for all values of ρ in the range [0,1]. Notice that this correlation matrix is a special case of a Toeplitz correlation structure. For example, toeplitz({1 .2 .2 .2}) is a valid correlation matrix. This is good to keep in mind, because sometimes it is hard to generate a positive definite matrix
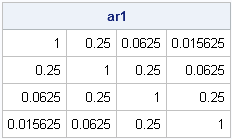
A covariance matrix with first-order autoregressive (AR1) structure
A first-order autoregressive (AR(1)) structure is a Toeplitz matrix with additional structure. Whereas an n x n Toeplitz matrix has n parameters, an AR(1) structure has two parameters. The values along each diagonal are related to each other by a multiplicative factor. The following module generates a matrix with AR(1) structure by calling the module in the previous section:
start AR1(dim, s, rho); u = cuprod(j(1,dim-1,rho)); /* cumulative product */ return( s##2 # toeplitz(1 || u) ); finish; ar1 = AR1(4, 1, 0.25); print ar1; |

4 Comments
Pingback: Constructing block matrices with applications to mixed models - The DO Loop
Pingback: Vectorizing the construction of a structured matrix - The DO Loop
Pingback: Visualize a matrix in SAS by using a discrete heat map - The DO Loop
Pingback: An explicit formula for eigenvalues of an AR(1) correlation matrix - The DO Loop