In my recent article on simulating Buffon's needle experiment, I computed the "running mean" of a series of values by using a single call to the CUSUM function in the SAS/IML language. For example, the following SAS/IML statements define a RunningMean function, generate 1,000 random normal values, and compute the running mean for the 1,000 points:

proc iml;
/* compute running mean of a vector: m[i] = mean(x[1:i]) = sum(x[1:i]) / i; 
   Assume no missing values and assume a row vector */
start RunningMean(x);
   return( cusum(x)/(1:ncol(x)) );
finish;
 
call randseed(123); 
x = j(1,1000);   /* allocate 1x1000 vector */
call randgen(x,"Normal"); /* fill with random values from std normal */
rm = RunningMean(x);

When I programmed the running mean, I wondered if this idea could be generalized to higher moments (variance, skewness, and so forth) in the same elegant manner. For example, can you similarly vectorize the variance formula so that, given a vector x of values, you compute a vector quantity, v such that v[i] is the variance of x[1:i]? Such a computation would enable you to efficiently compute and plot the running mean and the running variance together, as shown in the following graph:

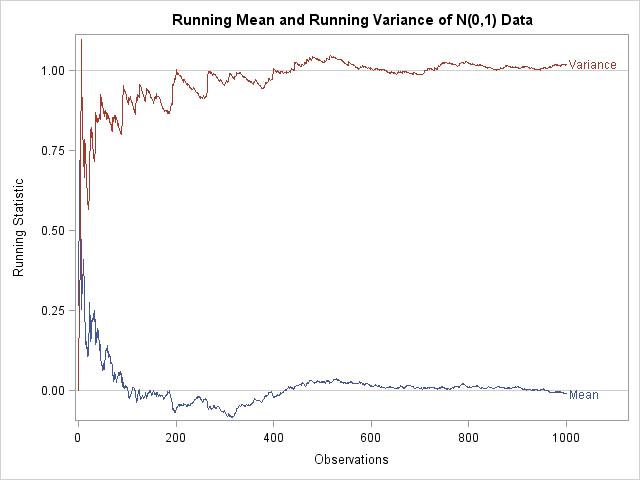
I decided that, technically, any one-pass algorithm can be used to compute a running statistic, and one-pass algorithms for computing basic moments are well-known. (In fact, many are implemented in PROC MEANS in SAS!) I also remembered seeing a note on John D. Cook's blog about computing a running variance. A different formula appears in Sheldon Ross's book, Simulation (p. 116, Eqn 7.6 and 7.7 of the Second Edition), where it is used to monitor the Monte Carlo standard error in order to determine when to halt a simulation.

I thought it might be fun to implement the running variance in SAS/IML, with the goal of vectorizing the computation, rather than computing it in a loop. The first thing I did was to compute the correct answer by writing a function that calls the VAR function in a loop for the vector x[1:i]:

/* compute running variance of a vector:
   s[i] = var(x[1:i]) = ssq(x[1:i] - mean(x[1:i])) / (i-1); 
   Assume no missing values and assume a row vector.
   Naive approach: DO NOT USE */
start NaiveRunningVar(x);
   n = ncol(x);
   s = j(1,n,.);
   do i = 2 to n;
      s[i] = var( x[1:i] );
   end;
   return( s );
finish;

This module serves as a reference in two ways: (1) I know that it computes the correct answer, and (2) I can compare the time required by the "naive" (=slow) module and a future vectorized version.

I decided to try to vectorize Ross's recursion formula. Ross's formula for a running variance is given by the following SAS/IML statetments:

/* Ross's method: p. 116 of _Simulation_ */
start Ross(x);
   N = ncol(x);
   M = RunningMean(x);
   S = j(1,N,0); /* allocate running variance */
   do k = 2 to N;
      *M[k] = M[k-1] + (x[k] - M[k-1])/k; /* use vectorized running mean instead */
      S[k] = (1 - 1/(k-1))*S[k-1] + k*(M[k] - M[k-1])##2;
   end;
   S[1] = .; /* convention: set S[1]=. */
   return (S);
finish;

Ross's formula is inside the DO loop. The first recursion relationship (which is commented out) computes the running mean. The second relationship, which involves the S variable, computes the running variance in terms of the squared difference between the previous two terms of the running mean. The formula suggests that you can probably compute the vector (M - lag(M,1))##2 and use the cumulative sums of its terms to compute a vectorized formula for the running variance. The LAG function, which is available in SAS/IML 9.22, computes a lagged (shifted) vector. In fact, the quantity M - lag(M,1) can be written more compactly as dif(M,1), which uses the DIF function.

A little bit of algebra led me to the following formula for the kth term of the running variance:

(k-1)S_k = Σ^k_i=1 i(i-1)(M_i - M_i-1)²

With this result, I can write the running variance in a vectorized form, as shown in the following function:

/* compute running variance of a row vector:
   m[i] = var(x[1:i])    (assuming no missing values) */
start RunningVar(x);
   N = ncol(x);
   M = RunningMean(x);
   D = (1:N) # (0:N-1) # T(dif(M,1))##2;
   return( cusum(D) / ( 1 || (1:N-1) ));
finish;
 
/* check answers */
S = RunningVar(x);
Ross = Ross(x);
S1 =  NaiveRunningVar(x);
maxDiff1 = max(abs(Ross-S)); /* compare with Ross's recursion formula */
maxDiff2 = max(abs(S1-S));   /* compare with naive method */
print maxDiff1 maxDiff2;

The answers are the same for all three methods. I'm excited by this vectorized formula! Perhaps someone else has written it down, but I haven't seen it. If you find another vectorized formula for the running variance, please provide the reference in the comments.

In terms of timing, the vectorized algorithm is almost instantaneous (less than 0.1 seconds) for vectors up to a million elements. As expected, the naive algorithm scales poorly, requiring more than six seconds for a vector that contains 50,000 elements. The Ross recursion relationship that uses a DO loop scales linearly with the number of elements, but is still not as efficient as the vectorized algorithm. The following graph plots computation time versus the number of elements:

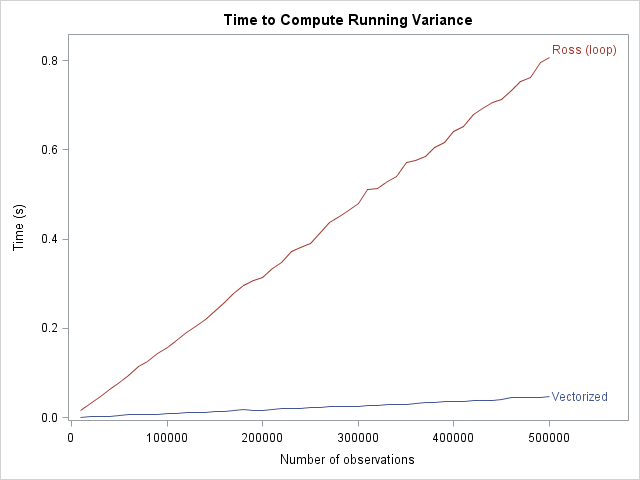
Notice that doing a half-million computations in PROC IML is fast (0.8 of a second), so it is not strictly necessary to vectorize this computation. Still, the vectorized algorithm is even faster. The difference in slopes between the two loops is the relative cost of iterating over elements in a DO loop instead of performing a single vector operation.