Last week I showed a graph of the number of US births for each day in 2002, which shows a strong day-of-the-week effect. The graph also shows that the number of births on a given day is affected by US holidays. This blog post looks closer at the holiday effect. I actually conducted this analysis in 2009 for my book, but decided not to include it.
I want to identify days in 2002 that have fewer births than would be expected, given the day of the week. A box plot is often used for this sort of exploratory data analysis. The following statements use the VBOX statement in the SGPLOT procedure to create a box plot for each day of the week and to label the outliers for each day:
proc sgplot data=birthdays2002; title "US Births by Day of Week (2002)"; vbox Percentage / category=Day datalabel=Date; yaxis grid; xaxis display=(nolabel) discreteorder=data; run; |
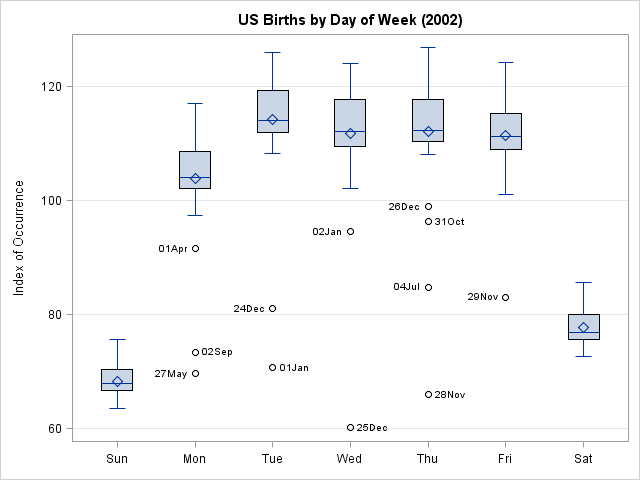
In the box plots (click to enlarge), the outliers for each day of the week are labeled by using values of the Date variable. Each date belongs to one of the following categories: US holidays, days near holidays, and inauspicious days.
US holidays
Several US holidays in 2002 are responsible for lower than expected births, given the day of the week:
- Tuesday, 01JAN (New Year's Day)
- Monday, 27MAY (Memorial Day)
- Thursday, 04JUL (Independence Day)
- Monday, 02SEP (Labor Day)
- Thursday, 28NOV (Thanksgiving Day)
- Wednesday, 25DEC (Christmas Day)
Christmas Day is the day on which the fewest babies were born.
Several "minor" holidays on Mondays also exhibit slightly smaller-than-expected births. These are not visible in the box plot graph, but can be seen in the time series graph: 21JAN (Birthday of Martin Luther King, Jr.), 18FEB (Washington's Birthday, sometimes known as "President's Day"), 14OCT (Columbus Day), and 11NOV (Veterans Day).
Days near holidays
Families often travel on days near holidays, and that includes doctors and other hospital staff. Several of these days are visible as outliers in the birth data.
- Wednesday, 02JAN (day after New Year's Day)
- Friday, 29NOV (day after Thanksgiving Day)
- Tuesday, 24DEC (Christmas Eve)
- Thursday, 26DEC (day after Christmas Day)
Friday, 03JUL (the day prior to Independence Day), also exhibits smaller-than-expected births, as seen in the time series graph.
Inauspicious days
The following dates are also outliers:
- Monday, 01APR (April Fool's Day)
- Thursday, 31OCT (Halloween Day)
Most parents don't want their child to be teased for being an "April Fool" all his life. It is less clear why a couple would avoid giving birth on Halloween. Superstition? Maybe. Or maybe doctors don't induce deliveries on Halloween so that they can be home for trick-or-treating?
These days might not be preferred for giving birth, but these are both blog-able holidays: I've written Halloween posts and April Fool posts.
Interestingly, for leap years, 29FEB also falls into the "inauspicious day" category. I guess parents avoid that date because the poor child would only get birthday parties every four years? Personally, I think it would be fun to be born on a leap day. And think how impressed people would be when I brag that I completed college before I celebrated my eighth birthday!

13 Comments
I did a similar analysis a while back, mostly as an exercise in Excel plotting techniques, and partly to refute the conclusion of a New York Times article:
Births by Day of the Year
Nice work...and remarkably similar conclusions! Well done.
Jon... is your Births by Day of the Year analysis still available online somewhere? The link in your comment doesn't work, and I would really love to have access to that analysis again. I had it saved at the time you did it and used to discuss it with my childbirth classes, but I seem to have misplaced it somewhere during computer changes. I hope it's still available online or, if not, would you be willing to email it to me? THANKS!
I'd think parents of newborns disproportionally are the parents of children aged 1 - 12 as well and probably have Halloween activities with their children.
I thought this was going to be a post on how many children were born 9 months after a holiday. That's an analysis I'd be interested in seeing
Well, as someone else commented, September is nine months after New Year's Eve. April/May is nine months after...what? Back to School? Or National Ice Cream Sandwich Day?
This was 2002 data. April/May is 9 months after 9/11.
Affirmation of life as a response to tragedy seems likely.
It's true! When my daughter was about 10, she realized that all of my grandmother's children were born in mid-September to early October. She knew pregnancy lasted about nine months so she counted backward and came up with a rather personal question for my grandmother. She thought she'd catch my grandmother off guard, but she got a little surprise when the conversation went like this:
Daughter: Grandmama, why are all of your kids born in September and October? Couldn't you and Granddaddy find some other way to entertain yourselves in December and January?
Grandmama: Well, you know we were pretty poor back in those days, and I couldn't afford to buy Granddaddy a present for Christmas... so I just had to give him what I had lying around the house.
Daughter: Oh. Ohhhhhhhh... ewwwww!
Grandmama: ::cackles uncontrollably::
;-)
Very interesting ... I'm not sure how parents control when their baby is born. I'll be curious to see your follow-up analysis on most successful delay methods. :-)
The control is not at conception, it is at delivery time through induced deliveries and C-sections. You can't really "delay," you can only "speed up."
I wonder if part of the issue with holidays is that some psychological factor causes a delay (or early delivery for that matter), much like a woman's period can be delayed by stress or other psychological factors. I don't think a delay is completely out of the question.
What if you made a separate box for "holidays"?
Pingback: Vectorized computations and the birthday matching problem - The DO Loop
Pingback: The most likely birthday in the US - The DO Loop