Every year near Halloween I write a trick-and-treat article in which I demonstrate a simple programming trick that is a real treat to use. This year's trick features two of my favorite functions, the CUSUM function and the LAG function. By using these function, you can compute the rows of a matrix (or indices of a vector) that correspond to the beginning and end of groups.

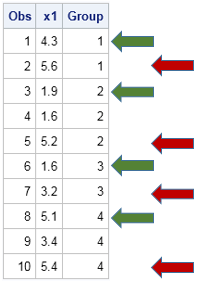
The picture at left illustrates the problem to solve. You have data that contains a grouping or ID variable, and you want to find the first and last observation that corresponds to each group. In the picture, the ID variable is named Group. The beginning the groups are indicated by the green arrows: rows 1, 3, 6, and 8. The end of the groups are located at the red arrows: rows 2, 5, 7, and 10.

Often it is the case that you already know the sizes of the groups from some previous calculation. If you know the sizes, the CUSUM and LAG functions enable you to directly construct the vectors that contain the row numbers. (Of course, if the group sizes are all equal, you can easily solve this problem by using the DO function.)

Recall that the CUSUM function computes the cumulative sum of the elements in a vector. I've used the CUSUM function in more than a dozen blog posts over the years. The LAG function shifts a vector of values and is useful for any vectorized operations that involve comparing or manipulating adjacent values.

To see the CUSUM-LAG trick in action, assume that you know the sizes of each group. For the example in the picture, the group sizes are 2, 3, 2, and 3. The following function returns the vector of rows that begin and end each group::

proc iml;
/* Return kx2 matrix that contains the first and last elements 
   for k groups that have sizes s[1], s[2],...,s[k]. The i_th row contains
   the first and last index for the i_th group. */
start ByGroupIndices( s );
   size = colvec(s);              /* make sure you have a column vector */
   endIdx = cusum(size);          /* locations of ending index */
   beginIdx = 1 + lag(endIdx);    /* begin after each ending index ... */
   beginIdx[1] = 1;               /*    ...and at 1  */
   return ( beginIdx || endIdx );
finish;
 
size = {2, 3, 2, 3};              /* sizes for this example */
idx = ByGroupIndices(size);
print idx[c={"Begin" "End"}];

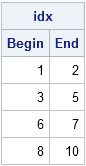
The CUSUM function computes the end of each group by accumulating the group sizes. The LAG function merely returns a vector of the same size, but with a missing value in the first element and all other elements shifted down one position. To that vector, you add 1 because the next group starts immediately after the previous group ends. Lastly, you just replace the missing value in the first position with 1 because the first group starts at the first row.

I've used the CUSUM-LAG trick many times. It is useful when you are simulating data in which the size of the sample is also being simulated. For example, just last week I used it to simulate contingency tables. Several years ago I used this trick to expand data by using frequencies. In general, you can use it as an alternative to the UNIQUEBY statement to perform "BY-group processing" in the SAS/IML language.

Happy Halloween to all my readers. I hope you find this trick to be a real treat!