In my article on Buffon's needle experiment, I showed a graph that converges fairly nicely and regularly to the value π, which is the value that the simulation is trying to estimate. This graph is, indeed, a typical graph, as you can verify by running the simulation yourself.

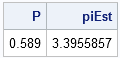
However, notice that the graph dips down to about π after about 300 iterations before increasing. This means that you could cheat. You could run the simulation for about 300 iterations and proclaim "Look how well this method does! And it only took 300 iterations!" In fact, if you use exactly 321 iterations, the estimate for π is 3.145, which is pretty close to the true value.

Here's another way you can cheat with this simulation: change the random number seed. Suppose that you wanted to cast doubt on this method of estimating π. You could change the random number seed and rerun the program until you get a result that appears to a horrible estimate. For example, if you rerun the program with the random number seed 12345 (that is, call randseed(12345)), the graph is the following:

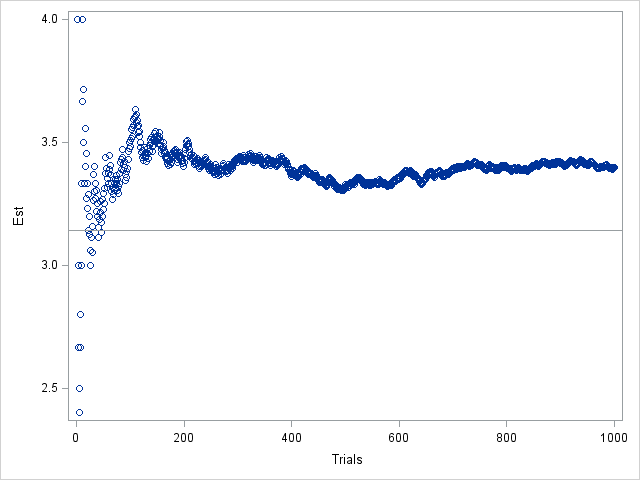
Not only is the estimate for N=1000 far from π, but the graph looks like it has converged to an entirely different value. If you are developing the algorithm and you see the previous graph, you might erroneously think that there is a bug in your program.

Of course, if you run the program for, say, 50000 iterations, you will see that the graph does eventually converge to the value π, as shown in the following graph that uses the same "bad" seed:

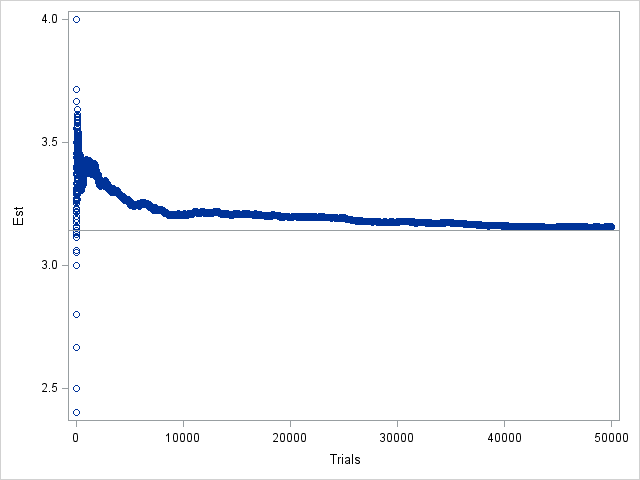
These graphs tell an important cautionary tale and remind us that samples—even simulated samples!—contain sampling variability. Therefore, be cautious of claims that are based on a single run of a simulation. Also, when you write a simulation, you should occasionally change the random number seed, just to see how the seed affects the simulation.

Another conclusion to draw is that it is important to know the variance of your estimator. Brian Ripley in his book Stochastic Simulation (1987, p. 194) shows that the variance of this estimator is approximated by 5.63/N, which is quite large. A 95% confidence interval for the parameter is Estimate ± 1.96 sqrt(5.63/N), which means that about 200,000 iterations are required to achieve an estimate that is probably within ±0.01 of π. (With 200,000 iterations, the estimate with the seed 12345 is 3.1475.)

By the way, there are other "Buffon's needle estimators" that correspond to different experimental conditions and that have smaller variance, but, nevertheless, "because of the convergence rate 1/sqrt(N), Monte Carlo methods are ... not a serious way to determine π" (Ripley, p. 197).

So, next time that someone else shows you the results of a simulation, make two requests:

1. Ask to see several runs with different initial seeds. This is easily done by changing the random seed to 0, which means that the random number generator is initialized by the system time.
2. Try to determine the variance of the estimator so that you can compute the Monte Carlo standard error. This enables you to calculate the number of iterations that you need in order to estimate a parameter to within a certain tolerance. However, the number of iterations is based on a 95% confidence interval, so there is no guarantee.