Recently a SAS/IML programmer asked a question regarding how to perform matrix arithmetic when some of the data are in vectors and other are in matrices. The programmer wanted to add the following matrices:
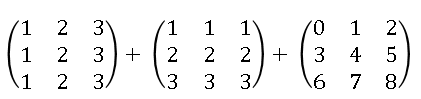
The problem was that the numbers in the first two matrices were stored in vectors. The programmer really had two vectors and a matrix that looked like this:
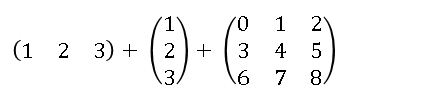
If you run the following PROC IML statements, SAS/IML reports that that "the matrices do not conform to the operation," which is a fancy way of saying that the dimensions of the various matrices are not compatible for addition:
proc iml;
x = {0 1 2,
3 4 5,
6 7 8};
r = 1:3; /* row vector */
c = t(1:3); /* column vector */
y = r + c + x; /* ERROR! */ |
Adding a vector to a matrix is not mathematically defined. However, this situation arises frequently in statistical computations with matrices. (For example, to center each column of a matrix, you subtract the mean of each column—a row vector—from the matrix.) Consequently, matrix languages support "shortcuts" for these operations, including convenient functions that "coerce" a vector into a matrix.
For this example, there are two easy solutions. One is to use the REPEAT function to reshape the vectors into square matrices. In other words, you manually create the matrices that are shown in the first image in this article. The following statements define a helper function that you can use to "expand" a vector into a square matrix. The number of columns in the vector determines how many new rows are created; the number of rows in the vector determines how many new columns are created. Thus a row vector (one row, many column) gets duplicated down, whereas a column vector (many rows, one column) gets duplicated across./* form square matrix from row vector or column vector */ start MakeMatrix(v); return( repeat(v, ncol(v), nrow(v)) ); finish; MatrixR = MakeMatrix(r); MatrixC = MakeMatrix(c); print MatrixR, MatrixC; |
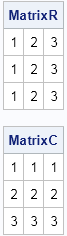
With these matrices defined, forming the sum is easy:
y = MakeMatrix(r) + MakeMatrix(c) + x; /* manually coerce vectors to matrices */ |
The second option is even easier. The SAS/IML language supports adding matrices and vectors provided that they have compatible dimensions. Consequently, if you rearrange the order of the SAS/IML variables so that the matrix appears first, then the expression is corrected interpreted and computed without physically forming any temporary matrices, as follows:
y = x + r + c; /* let SAS/IML coerce vectors for you */ |
I prefer the second solution because it is more efficient and does not require any extra memory. However, the MakeMatrix function is a useful little trick that is worth remembering.

5 Comments
Thanks Rick, I think you have converted me! I have been experimenting and brackets seem to be a problem as they change the order of evaluation. So something like:
.
y = x / (r + c);
.
does not work. Should there be a function to coerce an expression to the shape of another matrix? For example, I would like to be able to write something like :
.
y = x / coerce(r + c, x);
Because of order of evaluation, you have to tell the IML language what you mean by r+c. You might want a matrix, but others might want a vector. For example, someone might want to use the ROWVEC or COLVEC functions to write
y = x/(colvec(r)+c);
Another (semi-random) thought: the SHAPE function "repeats values as needed" in order to achieve a desired shape:
m = shape(r,n,m);
The IML development team is always open to suggestions to improve the language. If you think it would be useful, send me an email describing the proposed COERCE function and how you envision it would work.
Hi Rick. I need to know how I can produce a matrix with the following formula:
1/2+sum of "factorials" of row1-row3. That is to say, I have a matrix with let say 3 columns and 2 rows and I need to produce a new matrix by calculating a value for e.g. element from 1st row and 1st column is equal to (value in the cell=v(row,column)): 1/2+v(1,1)+v(1,1)*v(2,1). And 1st row 2nd column: 1/2+v(1,2)+v(1,2)*v(2,2). And 2nd row 1st column is purely: 1/2+v(2,1). And so on.
You can ask qustions like this at the
I was thinking that using basic matrix operations (an outer product by a unit vector) would also do the trick for expanding the matrices instead of repeat. For example:
a = {1 2 3};
R = j(3, 1, 1)*a;
reproduces your matrix R and
b = {1, 2, 3};
C = b*j(1, 3, 1);
reproduces your matrix C.