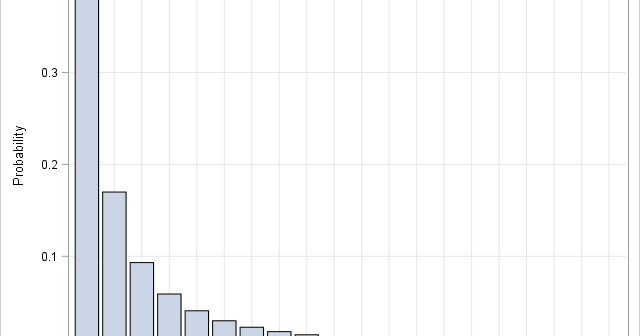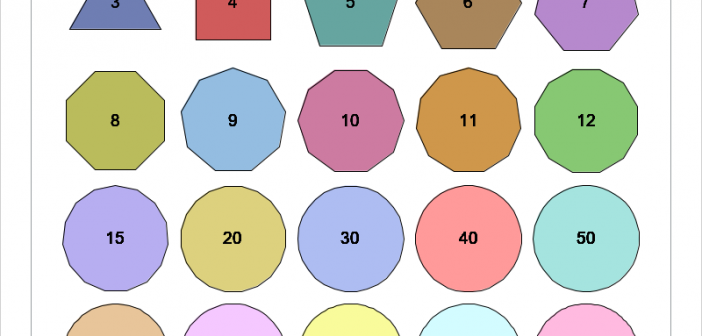
Recently, I saw a graphic on Twitter by @neilrkaye that showed the rapid convergence of a regular polygon to a circle as you increase the number of sides for the polygon. The author remarked that polygons that have 40 or more sides "all look like circles to me." That is,
This article discusses how to restrict a multivariate function to a linear subspace. This is a useful technique in many situations, including visualizing an objective function that is constrained by linear equalities. For example, the graph to the right is from a previous article about how to evaluate quadratic polynomials.
There are several different kinds of means. They all try to find an average value from among a set of numbers. Although the most popular mean is the arithmetic mean, the geometric mean can be useful for problems in statistics, finance, and biology. A common application of the geometric mean
What is this math good for, anyway? –Every student, everywhere I am a professional applied mathematician, yet many of the mathematical and statistical techniques that I use every day are not from advanced university courses but are based on simple ideas taught in high school or even in grade school.
The eigenvalues of a matrix are not easy to compute. It is remarkable, therefore, that with relatively simple mental arithmetic, you can obtain bounds for the eigenvalues of a matrix of any size. The bounds are provided by using a marvelous mathematical result known as Gershgorin's Disc Theorem. For certain
Last week I compared the overhand shuffle to the riffle shuffle. I used random operations to simulate both kinds of shuffles and then compared how well they mix cards. The article caused one my colleague and fellow blogger, Rob Pratt, to ask if I was familiar with a bit of
Given a rectangular grid with unit spacing, what is the expected distance between two random vertices, where distance is measured in the L1 metric? (Here "random" means "uniformly at random.") I recently needed this answer for some small grids, such as the one to the right, which is a 7 x 6
Continued fractions show up in surprising places. They are used in the numerical approximations of certain functions, including the evaluation of the normal cumulative distribution function (normal CDF) for large values of x (El-bolkiny, 1995, p. 75-77) and in approximating the Lambert W function, which has applications in the modeling
My colleague Robert Allison recently blogged about using the diameter of Texas as a unit of measurement. The largest distance across Texas is about 801 miles, so Robert wanted to find the set of all points such that the distance from the point to Texas is less than or equal
Back in high school, you probably learned to find the intersection of two lines in the plane. The intersection requires solving a system of two linear equations. There are three cases: (1) the lines intersect in a unique point, (2) the lines are parallel and do not intersect, or (3)
