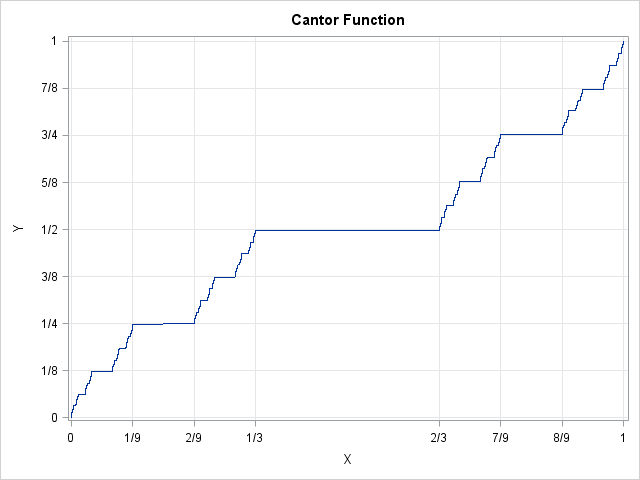
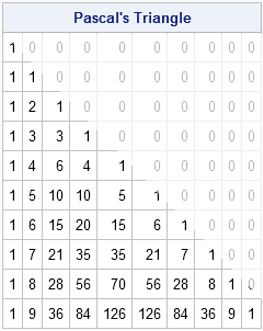
Out of the bosom of the Air, Out of the cloud-folds of her garments shaken, Over the woodlands brown and bare, Over the harvest-fields forsaken, Silent, and soft, and slow Descends the snow. "Snow-flakes" by Henry Wadsworth Longfellow Happy holidays to all my readers! In my last post I showed
I have a fondness for fractals. In previous articles, I've used SAS to create some of my favorite fractals, including a fractal Christmas tree and the "devil's staircase" (Cantor ) function. Because winter is almost here, I think it is time to construct the Koch snowflake fractal in SAS. A
I was a freshman in college the first time I saw the Cantor middle-thirds set and the related Cantor "Devil's staircase" function. (Shown at left.) These constructions expanded my mind and led me to study fractals, real analysis, topology, and other mathematical areas. The Cantor function and the Cantor middle-thirds
