You might have seen my previous blog, where I plotted some interesting tourist attractions on a geographical map of the British Isles (which may be of interest to Analytics 2013 Conference delegates)...
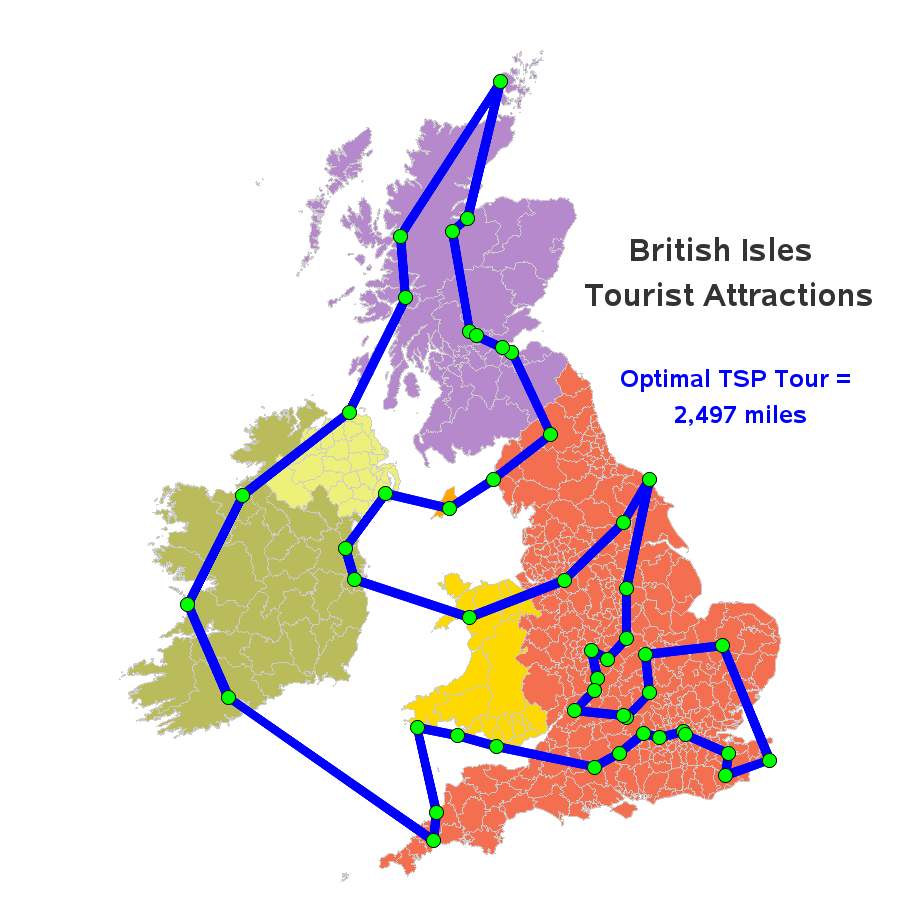
Well this blog uses even more powerful analytics, and shows how SAS can calculate the "optimal tour" to visit all the locations using the TSP statement in SAS/OR’s PROC OPTNET (the TSP statement invokes an algorithm that solves the traveling salesman problem).
First I generate every pair of locations (attractions), using PROC SQL. And while doing that, I also calculate the distance (in miles) between the latitude/longitude coordinates using the geodist function:
proc sql; create table pairs as select a.attraction as attraction1, a.lat as lat1, a.long as long1, b.attraction as attraction2, b.lat as lat2, b.long as long2, geodist(lat1, long1, lat2, long2, 'DM') as distance from attractions as a, attractions as b where a.attraction < b.attraction;Now we can ask PROC OPTNET to find the optimum tour (via the TSP statement), using the distance as the 'weight':
proc optnet data_links=pairs out_nodes=PathOrder; data_links_var from=attraction1 to=attraction2 weight=distance; tsp out=Path; (And, of course, this example assumes you can go straight from one tourist attraction to the next, using a helicopter or other James Bond-like flying device!)The rest of the code is just 'details' - using annotate move/draw functions to connect the points and such!
Did you know SAS could do this kind of "geographical analytics?" Perhaps you have some data you could analyze with the new PROC OPTNET?...

4 Comments
Pingback: How could SAS be used to help find missing planes like Flight 370?
this one is interesting. how efficient is this algorithm?
Efficiency is one of the major goals in all of the SAS procedures! The SAS/OR 12.1 User's Guide says: "The underlying algorithms are highly efficient and can successfully address problems of varying levels of detail and scale."
For this particular example, Proc Optnet runs (on my laptop PC) in less than a second, as indicated in the SAS log ... "Processing the traveling salesman problem used 0.95 (cpu: 0.11) seconds".
Pingback: Tourist attractions near Analytics 2013 London | SAS Training Post