Students in introductory statistics courses often use summary statistics (such as sample size, mean, and standard deviation) to test hypotheses and to compute confidence intervals. Did you know that you can provide summary statistics (rather than raw data) to PROC TTEST in SAS and obtain hypothesis tests and confidence intervals? This article shows how to create a data set that contains summary statistics and how to call PROC TTEST to compute a two-sample or one-sample t test for the mean.

Run a two-sample t test for difference of means from summarized statistics

The documentation for PROC TTEST includes an example that shows how to compute a two-sample t test for the difference between the means of two groups. Rather than repeat the documentation example, let's compare the mean heights of 19 students based on gender. The data are contained in the Sashelp.Class data set.

To use PROC TTEST on summary statistics, the statistics must be in a SAS data set that contains a character variable named _STAT_ with values 'N', 'MEAN', and 'STD'. Because we are interested in a two-sample test, the data must also contain a grouping variable. The following SAS statements sort the data by the grouping variable, call PROC MEANS to write the summary statistics to a data set, and print a subset of the statistics:

proc sort data=sashelp.class out=class; 
   by sex;                                /* sort by group variable */
run;
proc means data=class noprint;           /* compute summary statistics by group */
   by sex;                               /* group variable */
   var height;                           /* analysis variable */
   output out=SummaryStats;              /* write statistics to data set */
run;
proc print data=SummaryStats label noobs; 
   where _STAT_ in ("N", "MEAN", "STD");
   var Sex _STAT_ Height;
run;

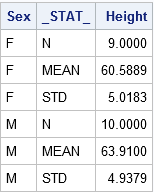
The table shows the structure of the SummaryStats data set for two-sample tests. The two samples are defined by the levels of the Sex variable ('F' for females and 'M' for males). The _STAT_ variable specifies the name of the statistics that are used in standard formulas for computing confidence intervals and hypothesis tests. The Height column shows the value of the statistics for each group.

You can use a data set like this one to conduct a two-sample t test of independent means. In a textbook, the problem is usually accompanied by a little story, like this:
The heights of sixth-grade students are normally distributed. Random samples of n₁=9 females and n₂=10 males are selected. The mean height of the female sample is m₁=60.5889 with a standard deviation of s₁=5.0183. The mean height of the male sample is m₂=63.9100 with a standard deviation of s₂=4.9379. Is there evidence that the mean height of sixth-grade students depends on gender?

The story suggests running a two-tailed test of the null hypothesis μ₁ = μ₂ against the alternative hypothesis that μ₁ ≠ μ₂. You do not have to do anything special to get PROC TTEST to use the summary statistics: if the procedure sees that the input data set contains a special variable named _STAT_ and the special values 'N', 'MEAN', and 'STD', then the procedure assumes that the data set contains summarized statistics. The following statements compare the mean heights of males and females for these students:

proc ttest data=SummaryStats order=data
           alpha=0.05 test=diff sides=2; /* two-sided test of diff between group means */
   class sex;
   var height;
run;

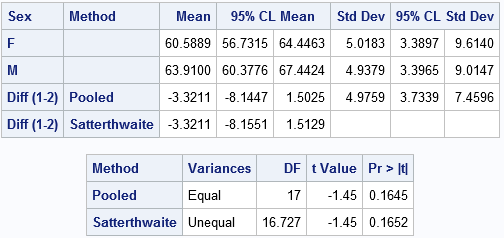
Notice that the output includes 95% confidence intervals for the group means, an estimate for the difference in means (-3.3211), and a confidence interval for the difference. You also get confidence intervals for the standard deviations.

In the second table, the "Pooled" row gives the t test under the assumption that the variances of the two groups are approximately equal, which seems to be true for these data. The value of the t statistic is t = -1.45 with a two-sided p-value of 0.1645. With this small sample, we fail to reject the null hypothesis at the 0.05 significance level. (For unequal group variances, use the "Satterthwaite" row.)

The syntax for the PROC TTEST statement enables you change the significance level and the type of hypothesis test. For example, to run a one-sided test for the alternative hypothesis μ₁ < μ₂ at the 0.10 significance level, you can use:

proc ttest ... alpha=0.10 test=diff sides=L;  /* Left-tailed test */

Run a one-sample t test of the mean from summarized statistics

In the previous section, PROC MEANS generated the summary statistics. However, you can also create the summary statistics manually, which is useful when you do not have access to the original data. As before, the key requirements are a variable named _STAT_ that has values 'N', 'MEAN', and 'STD'.

For example, a Penn State online statistics course states the following problem:
A research study measured the pulse rates of 57 college men and found a mean pulse rate of 70.4211 beats per minute with a standard deviation of 9.9480 beats per minute. Researchers want to know if the mean pulse rate for all college men is different from the current standard of 72 beats per minute.

The following SAS DATA step writes the summary statistics to a data set, then calls PROC TTEST to run a one-sample test of the null hypothesis μ = 72 against a two-sided alternative hypothesis:

data SummaryStats;
  infile datalines dsd truncover;
  input _STAT_:$8. X;
datalines;
N, 57
MEAN, 70.4211
STD, 9.9480
;
 
proc ttest data=SummaryStats alpha=0.05 H0=72 sides=2; /* H0: mu=72 vs two-sided alternative */
   var X;
run;

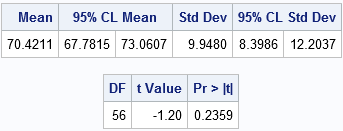
The results show that a 95% confidence interval for the mean contains the value 72. The value of the t statistic is t = -1.20, which corresponds to a p-value of 0.2359. Consequently, the data fails to reject the null hypothesis at the 0.05 significance level. These pulse rates are consistent with a random sample from a normal population with mean 72.

Summary

Although most people run PROC TTEST on raw data, you can also run PROC TTEST on summarized data. The procedure outputs the same tables and statistics as for raw data. You can run one- or two-sided tests for the mean value, or you can compare group means. When comparing the difference between group means, you can assume equal group variance ("Pooled" estimates) or unequal group variance ("Satterthwaite" estimates).

The only limitation when analyzing summary statistics is that PROC TTEST cannot produce ODS graphics because the graphics require the raw data.