A fundamental operation in statistical data analysis is to fit a statistical regression model on one set of data and then evaluate the model on another set of data. The act of evaluating the model on the second set of data is called scoring.
One of first "tricks" that I learned when I started working at SAS was how to score regression data in procedures that do not support the SCORE statement. I think almost every SAS statistical programmer learns this trick early in their career, usually from a more experienced SAS programmer. The trick is used in examples in the SAS/STAT User's Guide and on discussion forums, but it is not often explicitly discussed, probably because it is so well known. However,I had to search the internet for a while before I found a SUGI paper that describes the trick. In an effort to assist new SAS programmers, here is an explanation of how to score regression models by using the "missing value trick," which is also called the "missing response trick" or the "missing dependent variable trick."
Suppose that you want to fit a regression model to some data. You also have a second set of explanatory values for which you want to score the regression model. For example, the following DATA step create training data for the regression model. A subsequent DATA step creates evenly spaced values in the X variable. The goal is to evaluate the regression model on the second data set.
data A; /* the original data; fit model to these values */ input x y @@; cards; 1 4 2 9 3 20 4 25 5 1 6 5 7 -4 8 12 ; %let NumPts = 200; data ScoreX(keep=x); /* the scoring data; evaluate model on these values */ min=1; max=8; do i = 0 to &NumPts-1; x = min + i*(max-min)/(&NumPts-1); /* evenly spaced values */ output; /* no Y variable; only X */ end; run; |
The trick relies on two features of SAS software:
- The first data set contains variables X and Y. The second contains only X. If the two data sets are concatenated, a missing value is assigned to Y for each value of X in the second data set.
- When a regression procedure encounters an observation that has a missing value for the response variable, it does not use that observation to fit the model. However, provided that all of the explanatory variables are nonmissing, the procedure does compute the predicted value for that observation.
Consequently, the missing value trick is to concatenate the original data with the scoring data. If you call a regression procedure on the concatenated data, the original data are used to fit the data but predicted values are generated for the scoring data, as follows:
/* The missing response trick. 1. Concatenate the original data with the score data */ data B; set A ScoreX; /* y=. for all obs in ScoreX */ run; /* 2. Run a regression. The model is fit to the original data. */ proc reg data=B plots=(NONE); model y = x; output out=Pred p=P; /* predicted values for the scoring data */ quit; proc print data=Pred(obs=12); run; |
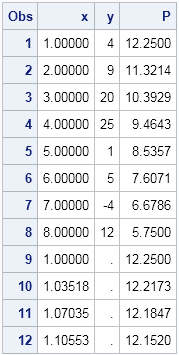
The table shows that the scoring data, which begins in row 9, contains predicted values as desired.
The advantage of this technique is that it is easy to implement. A disadvantage is this technique makes two extra copies of the scoring data, which might require a lot of disk space if the scoring data set is huge. A second disadvantage is that the trick increases the number of observations that the regression procedure must read. In the example, there are only eight observations in the original data, but the REG procedure has to read and write 208 observations.
There are other ways to evaluate a regression model, including using a SCORE statement, the SCORE procedure, and the relatively new PLM procedure. I will discuss these alternative methods in a future blog post.
I'm interested in hearing about when you first learned the missing response trick? Who did you learn it from? Do you still use it, or do you now use a more modern technique? Leave a comment.

6 Comments
Pingback: Techniques for scoring a regression model in SAS - The DO Loop
The missing value trick for scoring a regression model - The DO Loop
Rick,
Can you poll your readers to see people would like to see the above title as opposed to the current title
The DO Loop
in the email alert?
I would very much like to see an informative title if it is not too difficult.
Thanks and have a good weekend!
Wex
Great idea! I have passed your suggestion to the administrators. They will investigate what is possible.
Hi Rick!
how do you save the model estimates using proc genmod (for repeated measures analysis) in a file and then use this file/estimates to score data in a different session in SAS. I cannot import or export data, but can only transfer file with estimates for remote analysis due to data restrictions. I am not sure, but store statement/plm, score or proc score would not work. I appreciate your help!
Thanks!
Kay
STORE + PROC PLM is what I recommend. If that is not working for you, post your code and any error messages to the SAS Support Communities.
I just noticed this. You ask: "I'm interested in hearing about when you first learned the missing response trick?" I'm pretty sure I was using it during my first job where I had SAS available in the late 1980s.