I was recently asked, "Does SAS support computing inverse hyperbolic trigonometric functions?"

I was pretty sure that I had used the inverse hyperbolic trig functions in SAS, so I was surprised when I read the next sentence: "I ask because I saw a Usage Note that says these functions are not supported." [Editor's Note 16NOV2012: SAS Technical support has updated the Usage Note. Hurray!]

Sure enough, I followed the link and found an old Usage Note (which references a SAS newsletter article from 1993!) that states that SAS does not support the arc-hyperbolic trig functions!

Well, the Usage Note was correct when it was written many years ago, but it is wrong now. SAS added support for the inverse hyperbolic functions in SAS 9.2. Until I can get someone to revise that Usage Note, here's a quick list of the inverse hyperbolic functions in SAS:

• The ARCOSH Function computes the inverse hyperbolic cosine
• The ARSINH Function computes the inverse hyperbolic sine
• The ARTANH Function computes the inverse hyperbolic tangent
• The inverse hyperbolic secant at x is computed as ARCOSH(1/x)
• The inverse hyperbolic cosecant at x is computed as ARSINH(1/x)
• The inverse hyperbolic cotangent at x is computed as ARTANH(1/x)

And remember that you can call any Base SAS function from the SAS/IML language and pass in a vector of values. So, for example, you can evaluate the arc-hyperbolic tangent at uniformly spaced points in it's domain by using the following statements:

proc iml;
x = do(-0.99, 0.99, 0.01);
y = artanh(x);

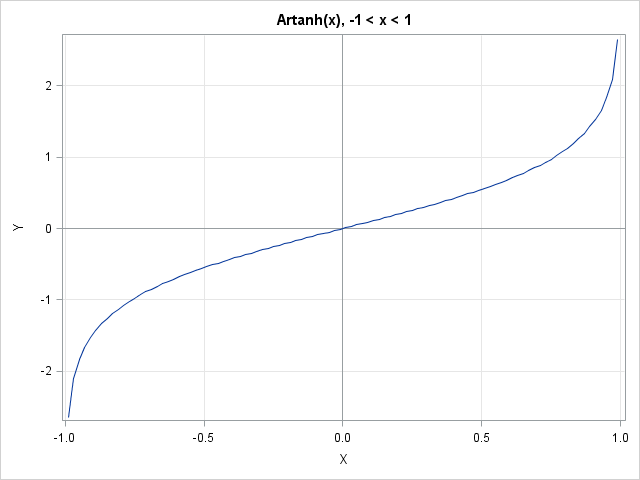
Notice that SAS does not have a function for the arc-hyperbolic secant, cosecant, or cotangent. Although, to be safe, I should say that it doesn't have those functions in SAS 9.3. In 10 years, who knows?